Atrodi dārgumus

Pirāts Pips meklē salā paslēptus dārgumus.

Pipam ir karte, kurā norādīts, kur atrodas dārgumi. Karte ir sadalīta 16 kvadrātos. Pips īpašā
ierīcē var ievadīt jebkuru kvadrātu skaitu, un ierīce viņam pateiks, vai dārgums atrodas kādā
no ievadītajiem kvadrātiem.

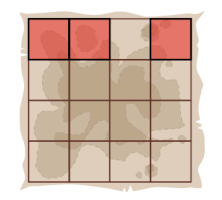
Piemēram, ja ierīce saka “jā”, kad Pips ievada izceltos kvadrātus, tas nozīmē, ka dārgums
atrodas vienā no šiem trim kvadrātiem:

Pips pēc iespējas ātrāk vēlas noskaidrot, kurā kvadrātā atrodas dārgumi.

Jautājums

Cik reizes Pipam ir jāizmanto ierīce, lai atrastu dārgumus pēc iespējas ātrāk?

Šī ir informātika

Metodi, ko Pips izmanto, lai atrastu dārgumu, datorzinātnē sauc par bināro meklēšanu. Termins “binārais” cēlies no latīņu valodas vārda “bis” (divreiz). Binārajā meklēšanā objekts tiek meklēts kopā, atkārtoti sadalot to uz pusēm, t. i., sadalot to divās daļās – no tā arī cēlies termins “binārais”. Kopu var labi sadalīt uz pusēm, ja tajā esošie objekti ir sakārtoti, piemēram, pēc lieluma; tas attiecas uz jebkuru skaitļu kopu, arī uz citām lietām. Tad kopa satur vidējo objektu, un jūs varat salīdzināt vidējo objektu ar meklējamo objektu. Ja vidējais objekts nav tas, ko meklējat, jūs vismaz zināt, kurā pusē atrodas meklētais objekts, un atkārtoti meklējat šo pusi bināri. Šādā veidā meklējamo objektu var atrast ļoti ātri. Ja ir 1 000 objektu, ir nepieciešami 10 meklēšanas soļi 2^9<1000<2^10, bet 1 000 000 objektu gadījumā – 20 soļi. Vispārīgi var teikt, ka n objektu meklēšanai ir nepieciešami aptuveni log(n) soļi; logaritma funkcija ir logaritms pie bāzes 2. Tā kā binārā meklēšana ir tik ātra, to bieži datorprogrammās izmanto meklēšanai sakārtotu datu kopās. Šajā uzdevumā meklēšanas telpa ir kvadrātukopa. Kvadrātus var sakārtot, tos numurējot no augšas uz leju un no kreisās puses uz labo. Tomēr šajā gadījumā var darboties arī, sadalot kopu uz pusēm kvadrātos, kuros vēl var atrast dārgumu. Tas tikai nedaudz apgrūtina atcerēšanos, kuru kvadrātu kopu vēl ir iespējams izmantot nākamajā meklēšanas posmā un kura atkal jāsadala uz pusēm.